Neural network-derived model accurately predicts oil recovery in water-drive reservoirs
The significant unknown when building ANN’s is the number of hidden layers and the number of neurons to include in the model. The generally accepted procedure is to make the ANN as simple as possible. For the majority of problems, one hidden layer is sufficient. With well-behaved data, it may be possible to minimize the neurons so that they are less than or equal to the number of inputs to the model—5 in the oil recovery factor case.
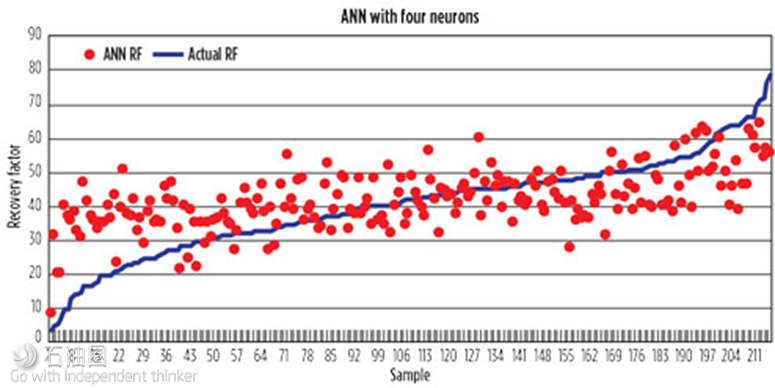
Unfortunately, it was found that when using a small number of neurons (<=5) the resulting ANN could not handle the recovery factor problem. Specifically, with a lower neuron count, the neural network was unable to model the high and low recovery factor trends, Fig. 4.
Since it appeared that the neural network had trouble finding an optimum solution that would cover the entire range of recovery factors for low neuron counts, multiple ANN models were built and evaluated. The objective was to find an optimum number of neurons that would yield a neural network that would generate values that were optimized over the entire range of expected recovery factors.
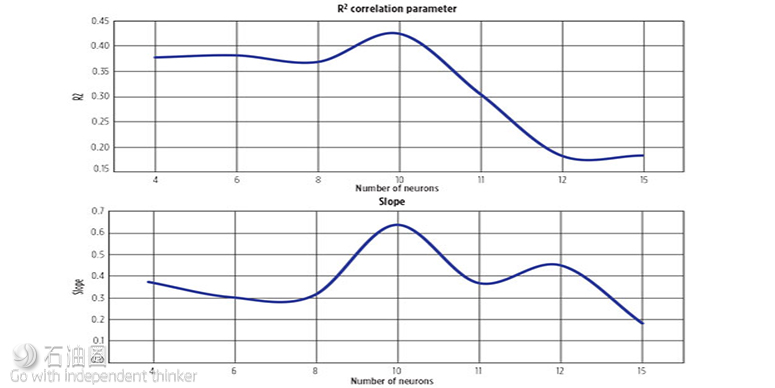
Figure 5 presents the slope and R2 correlation factor (actual RF vs ANN RF) for ANN’s built using different numbers of neurons. It appears that maximum accuracy of the ANN-calculated recovery factors occurs when the neural network contains ten neurons.
One caveat that should be kept in mind when considering the number of neurons to include is the potential of over-fitting the data. Neural network training is an exercise in fitting data to a complex mathematical function. If the function is made to match the training data too precisely by using a large number of neurons, then when independent data (blind test data) are run through the network, there is a risk that the results may not be acceptable.
The reason for this is that rather than generalizing patterns in the training data, the network has become a look-up table, because the neural network is too complex. In this situation, the ANN has essentially regenerated the input-output results used in training and cannot accurately process new inputs that are not within the look-up table. Keeping the caveat in mind, the final ANN Oil RF Model for sandstone reservoirs was built and trained with ten neurons.
SANDSTONE RESERVOIRS
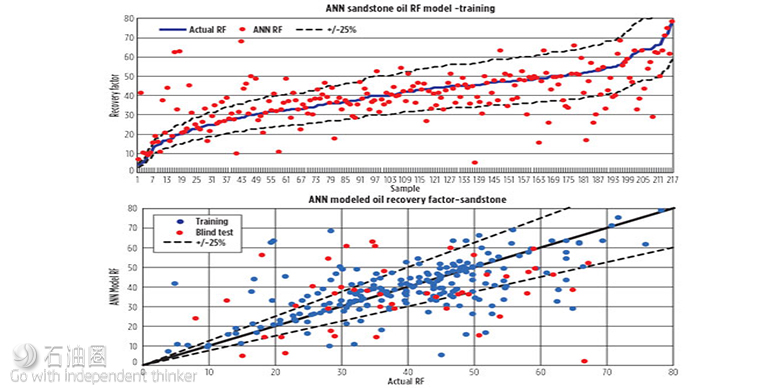
Figure 6 presents the actual recovery factors compared to the ANN-generated recovery factors for both the training and blind test data sets for sandstone reservoirs:
Sandstone reservoirs
10 non-linear neurons in ANN
Dataset: 264 reservoirs
Training/blind: 218/46
A random 20% of the training data set was used for validation checks during the training stage
The blind data set as not part of the training
Lines representing +/– 25% variation
Correlation coefficient is 0.59 (the outliers cause the correlation coefficient to be low).
After training the ANN Oil RF Model, 70% of the ANN calculated recovery factors were within +/–25% of the actual value.
The resulting equation that represents the ANN Oil RF Model for sandstone reservoirs is given in Fig. 7. The data ranges for the parameters used in the sandstone reservoir ANN Oil RF Model are as follows:
Oil in place: 10 MMbbl to 55,000 MMbbl
Permeability: 0.6 md to 7,000 md
Net pay: 10 ft to 1,800 ft
Porosity: 5% to 35%
Oil gravity: 15° API to 55° API
Oil viscosity: 0.1 cp to 88 cp.
Using input data outside the ranges presented above may yield unreasonable results. It should be kept in mind that even using input data within the ranges presented above may still yield results that are unreasonable, since there was not enough training data to cover all possible input combinations.
As an example of an ANN Oil RF model calculation, a sandstone water drive oil reservoir containing the following: STOOIP=10,000,000 bbl; permeability=10 md; net pay=50 ft; porosity=20%; Oil API=35°, and viscosity=0.13 cp is calculated to have an ANN recovery factor of 34.5%.
If the ANN Oil RF model is going to be used with missing data, then it may be valid to use an average value for the missing parameter. For the sandstone reservoir data set, the averages are as follows: Log(STOOIP) = 2.6524, Log(kh) = 4.3573, Log(viscosity) = 0.2167, Log(phi-h) = 3.2745 and Oil API = 33.5. If more than one of the parameters is missing, the ANN Oil RF Model should not be used.
CONCLUSIONS
An artificial neural network was built to generate recovery factors for sandstone oil reservoirs. The resulting model predicted the actual recovery factors within +/–25% for 70% of the data.
Although the results appear to be reasonable, there is still large scatter in the results. This is common for all recovery factor correlations and is the result of the variability, and averaging, of the input data.
As is the case for all recovery factor calculations, the results generated by the ANN Oil RF Model should be used with caution and checked against other techniques.
The ANN Oil RF Model represents the first step in generating a generic oil recovery factor model using artificial neural networks. The next step is to increase the size of the training data set and to further refine the training data.

 石油圈
石油圈