Neural network-derived model accurately predicts oil recovery in water-drive reservoirs
Artificial neural networks are information processing systems constructed to mimic procedures that resemble those of the human brain. They have the ability to learn procedures from training patterns or data. These systems excel at pattern matching, classification, data clustering and forecasting.
Artificial neural networks are well-suited for modeling complex non-linear relationships, including the modeling of oil recovery factors in water-drive reservoirs. Image: Apache Corp.
This theorum states that any continuous function that maps a set of real numbers, to another set of real numbers, can be approximated with a certain degree of accuracy by a feed-forward ANN with a single hidden layer and a finite number of hidden units, which contain non-linear transfer functions.
The first publicly available, general-purpose ANN designed specifically for the oil industry was called Neuro3 and was released by the DOE in 2001.2 It was rudimentary, but is still relevant.
The number of parts in the Vx Omni flowmeter has been reduced by approximately 66%, compared with previous-generation technologies. More than 90% of these components, including the most advanced instrumentation, are standardized for pressure rating, process fluids compatibility, temperatures, flow rates, and water depth.
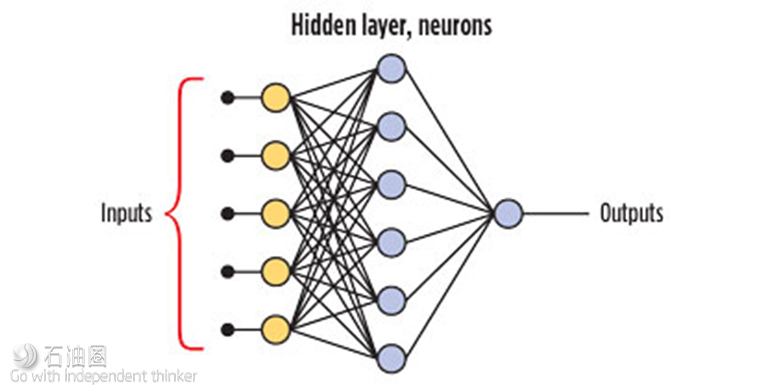
An ANN generates a predictive model as a multidimensional function containing elements with adjustable parameters. The most important elements of an ANN model are the neurons, which are contained in a “hidden layer,” Fig. 1. The neurons receive information in the form of numerical data input. This information is then combined with a set of parameters within the neural network to produce a result in the form of a numerical output.
Most common ANN models use a back-propagation, feed-forward, neural network system. The calculation procedure is feed-forward; in other words, from input layer through hidden layers to output layer. The back-propagation occurs during the training phase, where the calculated outputs are compared with the desired values, and the errors are input to modify the weights used in the ANN for the next iteration.
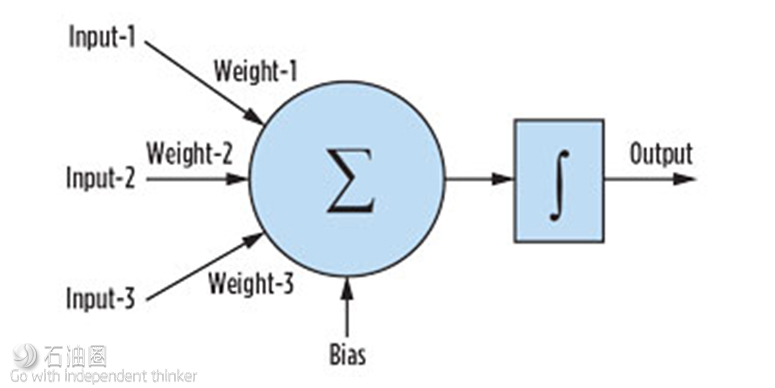
The neural network parameters are made up of two components: a “combination function,” which takes all the inputs and produces a set of net input values by calculating the combination of each neuron using a weight factor and a bias; and a “transfer function” which produces the neuron output. Figure 2 presents a single neuron feed-forward neural network process, where ∑ is the combination function and ∫ is the transfer function. It should be noted that the most common transfer function in predictive neural networks is the hyperbolic tangent (tanh).
Full-featured neural network programs are normally combined with genetic algorithms, statistics/linear regression, and fuzzy logic to automatically find optimal or near-optimal solutions for the problem.
The validity of any ANN model is dependent on how well the system has been trained. Normally, a large dataset of well-behaved data is used for training, and a different set of data is used as a blind test after the model is built. ANN systems will subdivide the training data set into a training set and a validating subset. This is not the same as using a data set as a blind test. The validating subset is still part of the training subset and is used in the back-propagation algorithms, so it is not an independent test of the model.
There are two steps in the development of a neural network: Training establishes the network structure and, the weight factors for the network and therefore, always occurs before the prediction step. Once trained, the ANN can be used to predict output data from new input.
OIL RECOVERY FACTOR
Artificial neural networks are particularly well-suited for modeling complex non-linear relationships, which cannot be easily patterned by traditional linear regression methods. SPE has published numerous papers on the use of neural networks in the oil industry. A search in www.onepetro.org, using the keywords “neural networks,” yields over 3,900 references.
The ANN oil recovery factor model was developed, using an open-source ANN system. There are free and commercial ANN programs available that are based on the open-source, OpenANN system, comprised of freely distributed neural network libraries.
Building the ANN Oil RF model. There are several empirical relationships that have been published for recovery factor predictions. The most common are the equations for recovery efficiency published by the API Subcommittee on Recovery Efficiency, developed from a statistical study of 70 water drive reservoirs.
The empirical API oil recovery factor equation for water drive (WD) oil reservoirs, for a given porosity (Ф), water saturation (Sw), formation volume factor (Boi), permeability (k), water viscosity (µw), oil viscosity (µoi), initial pressure (Pi) and abandonment pressure (Pab) is as follows:
An API RF equation description, and how it can be converted into a probabilistic determination of recovery factor, is described in the literature.
Based on general reservoir and production engineering principals, the parameters used to build the ANN Oil RF model were: sandstone reservoir, water drive, original oil in place (STOOIP), porosity (Ф), permeability (k), oil viscosity (µ), oil gravity (API) and net pay (h). Although these are not the only parameters that impact recovery, these parameters were considered to be the major components impacting long-term production and recovery of oil from a reservoir.
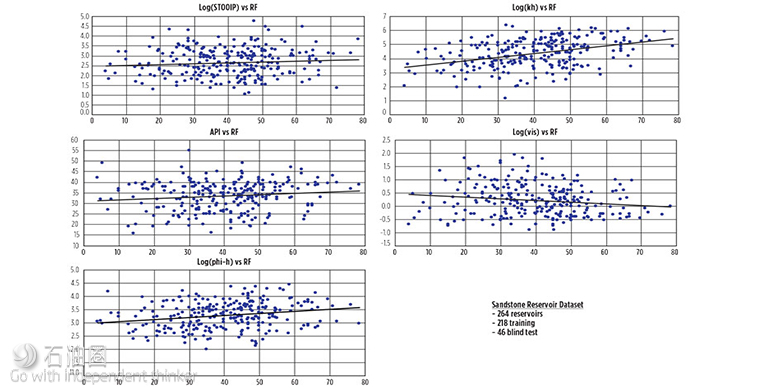
For the sandstone reservoir ANN Oil RF model, 264 sandstone/clastic water drive/combination drive oil reservoirs were available with complete data sets, including recovery factors. A random subset of 46 reservoirs was removed from the full data set, to be used as a blind test. Of the remaining 218 reservoirs, 20% were used as validating data for training. Figure 3 presents the data for the sandstone reservoir data set.
After a visual inspection, it becomes apparent that the data have a large scatter and a wide range. This is not unexpected when considering oil reservoir recovery factors. The scatter is one of the problems with trying to generate an oil recovery factor correlation that is universally valid. The scatter is predominantly caused by using average reservoir parameters, as well as the accuracy of the data.
To make the data more conducive to neural network use, the actual inputs to the ANN were: Log(STOOIP), Log(kh), Log(viscosity), Log(phi-h) and Oil API. The logarithm of the input data was used to linearize the data range and to place the maximum and minimum in a reasonable range, as well as to pre-process/linearize the data prior to use in the ANN.
Figure 3 shows that each input data set exhibits an approximate linear trend in terms of recovery factor. These apparent trends help the neural network system find an optimal solution. The original data set included 38 carbonate/dolomite oil reservoirs. These data were removed from the gross data set of 302 reservoirs, because the recovery factors calculated for the carbonate reservoirs were always the outliers in the resulting ANN model. This was the result of carbonate reservoirs containing natural fractures, which will impact the ultimate recovery from these reservoirs.

 石油圈
石油圈